Dynamic Programming

Introduction

Gosh hated doing this with LeetCode Patterns so this will not be fun.

Memorization

Not sure why this is referred to as this. You use memorization but you also us recursion

Fibonacci

So here is the almost famous Fibonacci code with recursion. The main thing is to make sure you cater for the base case.

const fib = (n) => {
 // First two numbers in Fibonacci are always 1
 if(n <= 2) return 1
 // Then the next value is the sum of the previous 2
 return fib(n-=1) + fib(n-2)
}

This takes forever when you use say 50 because of the stack. When we look at big O it is O(2ⁿ) time. Where n is 50 this works out to be 1.12e+15. To this faster we can draw it out and look for patterns and it some becomes clear we are doing things repeatably. A visualization makes this obvious

So to improve using memoiization by doing

const fib = (n, memo = {} ) => { 
 // Check if we have done this and just return the value
 if(n in memo) return memo[n]

 // First two numbers in Fibonacci are always 1
 if(n <= 2) return 1

 // Then the next value is the sum of the previous 2 and we store it
 memo[n] = fib(n-=1, memo) + fib(n-2, memo)

 // Now return
 return memo[n]

}

Caching this value means we bring the time complexity down to O(n). Greatly improving the speed.

GridTraveler

So here we are looking a grids where there maybe restrictions. e.g. cannot go up, cannot go back. In this example we can only go down or right.

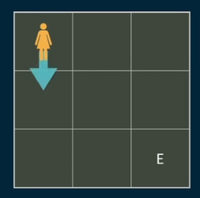
Here is the decision tree with the options and co-ordinates.

Now the code. This using recursion and stops when either out of bounds or destination achieved.

const gridTraveler = (m,n) => {
 
 // Hit base case (1,1)
 if(m == 1 && n == 1) return 1

 // Out of bounds
 if(m == 0 || n == 0) return 0

 // We have posibbly two choices 
 // keep going until you hit a base case
 return gridTraveler(m -1, n) + gridTraveler(m, n -1)
}

console.log(gridTraveler(3,2))

The height of the tree is driven by the two number inputs (n and m). To move down the tree we need to have increase m and increase n. So the height (number of levels) n + m. Because we have two choices per node (mostly) this is a binary tree and therefore we have 2x2x2 n+m times. So the time complexity is O(2^(m + n)). The space complexity is the height to O(n+m). So now we can review the tree and spot the duplicates. I guess what was interesting was identifying 1,2 and a 2,1 have the same number of nodes so gridTraveler(1,2) = gridTraveler(2,1).

const gridTraveler = (m,n, cache = {}) => {

 // Create a unique key for the current state
 const key = m  + '_' + n
 // Create flipped key
 const flippedKey = n + '_' + m

 // Check cache
 if(key in cache) return cache[key]
 if(flippedKey in cache) return cache[flippedKey]

 // Hit base case (1,1)
 if(m == 1 && n == 1) return 1

 // Out of bounds
 if(m == 0 || n == 0) return 0

 // We have posibbly two choices 
 // keep going until you hit a base case
 cache[key] = gridTraveler(m -1, n, cache) + gridTraveler(m, n -1, cache)
 return cache[key]
}

console.log(gridTraveler(3,2))
console.log(gridTraveler(18,18))

To calculate the reduction we can see we only now roughly calculate for the height x width which is m x n.

gridTraveler Complexity Comparison

Version	Time Complexity	Space Complexity	Notes	Example: gridTraveler(18,18)	Rough Speed
Brute Force	O(2m+n)	O(m + n)	Exponential calls; deep recursion stack	~68.7 billion calls	❌ Likely crashes or hangs; >10 minutes or stack overflow
Memoized (no flipped key check)	O(m × n)	O(m × n)	Stores both (m,n) and (n,m) separately	324 unique keys stored	✅ ~1–5 ms
Memoized (with flipped key check)	O(m × n)	O(m × n / 2)	Avoids redundant computation; halves cache size	~162 unique keys stored	✅ ~0.5–3 ms

Memoization Recipe

Suggestion was that you

• Make it work first
  • Visualize the problem as a tree
  • Implement the tree as recursion
  • Test it
• Make it efficient
  • Add a memo object
  • Add base case to return memo values
  • Store return values into the memo

CanSum

This where we have a value and an array. We return true if we can sum e.g.

canSum(7, [5,3,4,7]) -> true
canSum(7, [5,2]) -> false

So we end up with a tree like this.

So this took a lifetime to understand. The parent has too possible outcomes either line 11, hits a return true at any point if canSum or none is found and false is returned (line 15)

const canSum = (targetSum, numbers) => {
  // Exit recursion if targetSum is 0
  if (targetSum === 0) return true;
  
  // Exit recursion if targetSum is negative
  if (targetSum < 0) return false;

  for (const num of numbers) {
    const remainder = targetSum - num;
    // If we found a valid path, we can return true
    if (canSum(remainder, numbers) === true) return true;
  }

  // After doing all of the possible combinations, we return false
  return false;
};

const result = canSum(7, [5, 3, 4, 7]);
console.log("Result = ", result);

Looking for the complexity we see the height of the tree is m. We look at the branch factor they are around 3 or the length of the array. So O(n^m) for time and O(m) space

So now we now look to how to memoize it. To does this we

• Add a new base case to return memo if found
• Identify key - in this case targetSum
• Store targetSum/result for each return outside of base case
• Add memo to each call

HowSum

Next howSum. I am on to it and starting to like the process. So here is the function. With howSum we return the combinations which make the targetSum.

const howSum = (targetSum : number, numbers: number[]): number[]

So to do this we need so return something for each call

const howSum = (targetSum : number, numbers: number[]): number[] | null => {
    if(targetSum === 0) return []
    if(targetSum < 0) return null
    
    for(let num of numbers) {
        const remainder = targetSum - num 

        // Call for the n number in the array
        const remainderResult = howSum(remainder, numbers)

        // Check we are not null
        if(remainderResult !== null) {
            // Return the originally array plus the current number
            return [...remainderResult, num]
        }
    }

    return null
}
console.log("Result is", howSum(7, [5,3,4,7]));

So now for the memoization

const howSum = (targetSum : number, numbers: number[], memo = {}): number[] | null => {
    if(memo[targetSum]) return memo[targetSum]
    if(targetSum === 0) return []
    if(targetSum < 0) return null

    for(let num of numbers) {
        const remainder = targetSum - num 

        // Call for the n number in the array
        const remainderResult = howSum(remainder, numbers)

        // Check we are not null
        if(remainderResult !== null) {
            // Return the originally array plus the current number
            memo[targetSum] = [...remainderResult, num]
            return memo[targetSum]
        }
    }

    memo[targetSum] = null
    return null
}

console.log("Result is", howSum(7, [5,3,4,7]));

BestSum

So next is bestSum. Same deal but we track the shortest array. I have implemented the memo to save space.

const bestSum = (targetSum : number, numbers: number[], memo: { [key: number]: number[] | null }): number[] | null => {
    if(memo[targetSum]) return memo[targetSum]
    if(targetSum == 0) return []
    if(targetSum < 0) return null

    let shortestCombination: number[] | null = null

    for(let num of numbers) {
        const remainder = targetSum - num 

        // Call for the n number in the array
        const remainderResult = bestSum(remainder, numbers, memo)

        // Check we are not null
        if(remainderResult !== null) {
            // Return the originally array plus the current number
            const combination = [...remainderResult, num]
            // Update the shortest result if necessary
            if(shortestCombination === null || combination.length < shortestCombination.length) {
                shortestCombination = combination
            }
        }
    }

    memo[targetSum] = shortestCombination
    return shortestCombination
}

console.log("Result is", bestSum(7, [5,3,4,7], {}));

Again we can memorize so we have

Summary of can, how and best

These are categorised as

• canSum -> Decision Problem
• howSum -> Combinatoric Problem
• canSum -> Optimization Problem

CanConstruct

Next words. So this time we are given a word and a wordBank (array of words) and we need to determine if we can construct the word. So here is the tree.

So this was much the same a canSum. You just need to reduce the word until empty return true.

const canConstruct = (target: string, wordBank: string[], memo: { [key: string]: boolean }): boolean => {
    if (target === "") return true
    if (target in memo) return memo[target]

    for (const word of wordBank) {
        // JS provide indexOf
        if (target.indexOf(word) === 0) {
            const suffix = target.slice(word.length)
            if (canConstruct(suffix, wordBank, memo)) {
                memo[target] = true 
                return true
            }
        }
    }

    memo[target] = false
    return false;
}

console.log("Result is", canConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd"], {}));

CountConstruct

Track the totalCount. When the target becomes empty the word has been constructed so return 1.

const countConstruct = (target: string, wordBank: string[], memo: { [key: string]: number }): number => {
    if (target === "") return 1
    if (target in memo) return memo[target]

    let totalCount = 0

    for (const word of wordBank) {
        if (target.indexOf(word) === 0) {
            const suffix = target.slice(word.length)
            const currentCount = countConstruct(suffix, wordBank, memo)
            totalCount = totalCount + currentCount
        }
    }

    memo[target] = totalCount
    return totalCount;
}

console.log("Result is", countConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd", "ef"], {}));

AllConstruct

So the question is to return all valid combinations of valid arrays for a give word with a given word array.

const allConstruct = (target: string, wordBank: string[], memo: { [key: string]: string[][] }): string[][] 

There are two key things

a) when a branch does not match all the way to the bottom then it returns [] as target.indexof is not true
b) if the branch does match the array is assembled in reverse order.

const allConstruct = (target: string, wordBank: string[], memo: { [key: string]: string[][] }): string[][] => {
    if (target in memo) return memo[target]

    // No target return empty 2D array
    if (target === "") return [[]]

    // Initialize to empty 2D array, if target.indexOf(word) === 0 then [] is returned
    let result: string[][] = []

    // Iterate over each word (element) to the end
    for (const word of wordBank) {
        console.log("Doing word: %s", word)

        // If prefix not valid stop recursion
        if (target.indexOf(word) === 0) {

            // If prefix is valid, continue recursion
            const suffix = target.slice(word.length)

            // Call recursion with the suffix
            const suffixWays = allConstruct(suffix, wordBank, memo)

            // Build the array for each valid suffix way, prepend the current word
            const targetWays = suffixWays.map(way => [word, ...way])

            // Push the result
            result.push(...targetWays)
        }
    }

    // There is one array for each valid combination or empty array
    memo[target] = result
    return result;
}

console.log("Result is", allConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd", "ef"], {}));

Tabulation

Fib

Not really on board with this yes but there goes. For Fibonacci the approach was

• Create an array with n+1
• Initialize the array to zero
• Initialize first two to correct values 0,1 (seed)
• Iterate over the who array, adding value of i to elements, i+1, and i+2
• Return position n

const fib = (n) => {
    const data = Array(n+1).fill(0)
    data[1] = 1
    for (let i = 0; i < n; i++) {
        data[i+1] = data[i+1] + data[i]
        data[i+2] = data[i+2] + data[i]
    }
    return data[n]
}

console.log("Value:", fib(1))
console.log("Value:", fib(2))
console.log("Value:", fib(3))
console.log("Value:", fib(4))
console.log("Value:", fib(5))
console.log("Value:", fib(6))

Grid Traveler

So starting to understand. I need to think about the base cases and relate the choices for current position, in this case the choice are right and down.

const gridTraveler = (m,n) => {
    const rows = m +1
    const cols = n +1
    // Initialize m+1 x n+1 table
    const table = Array(rows).fill(0).map(() => Array(cols).fill(0))
    // We know Base Cases
    // at 0,0 we the is 0 ways to travel and 
    // at 1,1 there is 1 way to travel
    table[1][1] = 1
    // In the recursion code the next recursion consisted of
    // move down 1 and moving right 1
    // Let iterate over our table adding the current position to
    // a) column below b) row + 1
    for(let row =0; row < rows; row++) {
        for(let col=0; col < cols; col++) {

            if(col+1 < cols) {
                const newRow = table[row][col+1] + table[row][col]
                console.log("updating column+1 at %d,%d with value %d + %d =  %d", row, col+1, table[row][col+1] , table[row][col], newRow)
                table[row][col+1] += table[row][col]
            }

            if(row+1 < rows) {
                const newCol = table[row+1][col] + table[row][col]
                console.log("updating row+1 at %d,%d with value %d + %d =  %d", row+1, col, table[row+1][col] , table[row][col], newCol)
                table[row+1][col] += table[row][col]
            }
        }

    }
    console.log(table)
    return table[m][n]
}

console.log("Answer: ", gridTraveler(18,18));

Tabulation Recipe

• visualize the problem as a table
• size the table based on the inputs
• initialize the table with default values, e.g. 0, or false
• seed the trivial answers into the table
• iterate through the table
• fill further positions based on the current position

CanSum

Gosh this was tricky to get my head around. Why it works as the robot says. We are basically applying every number in the array to each possible answer. So if we had 7 target sum then the worst would be [1], i.e. 1+1+1+1+1+1+1+1+1

const tab_canSum = (targetSum,numbers) => {    
    const rows = targetSum+1
    const table = Array(rows).fill(false)

    // Base cases
    // targetSum = 0 == true
    table[0] = true

    for(let col=0; col < targetSum+1; col++) {
        
        // We only update if the current position is true
        if(table[col] === true) {
            // Iterate over numbers array
            for(let num of numbers) {
                // If inbounds update to true
                if(col+num <  targetSum+1) table[col+num] = true;
            }
        }
    }

    return table[targetSum]

}

console.log("Can Sum =", tab_canSum(7,[5,3,4,7]))
console.log("Can Sum =", tab_canSum(7,[5,3]))

HowSum

Still struggled to do this the first time through. Now I understand. Given the question is

tab_howSum(7, [5, 3, 4, 7]))

It works because you the program is updating the value in the appropriate slot using the number it has just read. Gosh bet I cannot understand this next time. We start with an empty array 8x1

0	1	2	3	4	5	6	7
[]	null	null	null	null	null	null	null

First time through we add the values from the array in there appropriate slot and this gives

0	1	2	3	4	5	6	7
[]	null	null	[3]	[4]	[5]	null	[7]

Notice each slot contains same number as the index. What happens from here is we iterate over the slots knowing the current slot always adds up to it's index.

Second time Slot 1, is null nothing done Third time Slot 2, is null nothing done Now we are on slot 3. 3 does have contain an array and it adds up to 3. We take each of our array numbers and combine it with the current slot. We do this because we want to create an index to move this to. We only put arrays in a slot where the numbers in the array add up to the slot index. We overwrite it there is already something in the slot.

0	1	2	3	4	5	6	7
[]	null	null	[3]	[4]	[5]	[3,3]	[4,3]

Notice each array adds up to its index.

const tab_howSum = (targetSum, numbers) => {
  // Create table
  const table = Array(targetSum+1).fill(null);

  // targetSum = 0 == true
  table[0] = [];
  
  // iterate of possible answers
  for (let i = 0; i < targetSum + 1; i++) {

    if (table[i] !== null) {
      for (let num of numbers) {
        if(i + num <= targetSum) table[i + num] = [...table[i], num];
      }

    }
  }
  return table[targetSum];
};

console.log("Can Sum =", tab_howSum(7, [5, 3, 4, 7]));

BestSum

This is becoming trivual but the main thing is we track the smallest for each possible number when updating

const tab_bestSum = (targetSum, numbers) => {
  // Create table
  const table = Array(targetSum + 1).fill(null);

  // targetSum = 0 == true
  table[0] = [];
  let shortestCombination = null;

  // iterate of possible answers
  for (let i = 0; i < targetSum + 1; i++) {
    if (table[i] !== null) {
      for (let num of numbers) {
        if (i + num <= targetSum) {
          // Only update if the current length is greater
          const current_length = table[i + num] === null ? targetSum : table[i + num].length;
          const new_length = [...table[i], num].length;
          if (current_length > new_length) {
            table[i + num] = [...table[i], num];
          }
        }
      }
    }
  }
  return table[targetSum];
};

console.log("Best Sum =", tab_bestSum(7, [5, 3, 4, 7]));
console.log("Best Sum =", tab_bestSum(8, [1, 4, 5]));

CanConstruct

First one I have done myself. Must be getting better at this.

const tab_canConstruct = (targetWord, wordBank) => {
  const rows = targetWord.length + 1;
  const table = Array(rows).fill(false);

  // Base cases
  // targetSum = 0 == true
  table[0] = true;

  for (let col = 0; col < targetWord.length + 1; col++) {

    if (table[col] === true) {

      // Iterate over words array
      for (let word of wordBank) {

        // Get the prefix
        const current_index = targetWord.slice(col).indexOf(word);

        // If we are a prefix
        if (current_index === 0) {
            console.log("Current slot:%d, setting slot %d to true for word %s",col, col + word.length,word);
            table[col + word.length] = true;
          // }
        }
      }
    } 
  }
  return table[targetWord.length];
};
console.log("Can Construct =", tab_canConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd"]));

CountConstruct

So here we are with count construct. Did this all myself again. Starting to feel chuffed.

const tab_countConstruct = (targetWord, wordBank) => {
  const rows = targetWord.length + 1;
  const table = Array(rows).fill(0);

  // Base cases
  table[0] = 1;

  for (let col = 0; col < targetWord.length + 1; col++) {

    if (table[col] > 0) {

      // Iterate over words array
      for (let word of wordBank) {

        // Get the prefix
        const current_index = targetWord.slice(col).indexOf(word);

        // If we are a prefix
        if (current_index === 0) {
            console.log("Current slot:%d, setting slot %d to true for word %s",col, col + word.length, word);
            table[col + word.length] = table[col]  + 1
          // }
        }
      }
    } 
  }
  return table[targetWord.length];
};

console.log("Can Construct =", tab_countConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd"]));

AllConstruct

Some sloppy mistakes mostly around the questions but all can right in the end.

const tab_allConstruct = (targetWord, wordBank) => {
  const rows = targetWord.length + 1;
  const table = Array(rows)
    .fill([])
    .map(() => []);

  // Base cases
  table[0] = [[]];

  // console.log(table);

  for (let col = 0; col < targetWord.length + 1; col++) {
      // Iterate over words array
      for (let word of wordBank) {
        // Get the prefix
        const current_index = targetWord.slice(col).indexOf(word);

        // If we are a prefix
        if (current_index === 0) {
            const newCombinations = table[col].map((curr)=> [...curr, word])
            table[col + word.length].push(...newCombinations)
        }
      }
  }
  return table[targetWord.length];
};

console.log("All Construct =",tab_allConstruct("purple", ["purp", "p", "ur", "le", "pupl"]));
console.log("All Construct =",tab_allConstruct("abcdef", ["ab", "abc", "cd", "def", "abcd","ef", "c"]));

// ABC
// [A, AB, C]

// 0 [[A], [AB]]
// 1 [[A], [AB]]
// 2 [[A, C], [AB, C]]

Iain's Final Thoughts

These questions were from freeCodeCamp on Dynamic Programming. Hist final thoughts were

• notice any overlapping subproblems (the same problem in maybe a different branch)
• decide what is the trivially smallest input
• think recursively to use memoization
• think iteratively to use tabulation
• draw a strategy first