LeetCode Patterns

Introduction

I always find patterns fascinating and just come out of write Grpc in Go, C#, Typescript, Rust and Java. So using approaches is a common thing for me. Filled this intro up so will press on.

A Picture Says A Thousands Words

Prefix Sum

Purpose

This is used to calculate the sum of an array between two ranges. E.g. you have the rating of a movie in an array from 0-6 and you want to figure out how did it do between day 2 and day 5. The idea is you hold the sum of each index in an array. So and array 1,2,3,4 you would calculate 1, 3, 6, 10. That way if you want 1-2 it would be p[2] - p[0] = 6-1 = 5

Concept

Given an input array `A` of length `n`, the prefix sum array `P` is defined as:

• `P[0] = A[0]`
• `P[i] = P[i-1] + A[i]` for `i > 0`

This allows fast computation of the sum of any subarray `A[l..r]` using:

• `sum = P[r] - P[l-1]` (with edge case handling for `l = 0`)

Implementation (JavaScript)

function prefixSum(arr) {
  const result = [];
  let sum = 0;
  for (let i = 0; i < arr.length; i++) {
    sum += arr[i];
    result.push(sum);
  }
  return result;
}

Example

Input:

const A = [3, 1, 4, 1, 5];
const P = prefixSum(A); // [3, 4, 8, 9, 14]

To compute sum of A[1..3] (i.e., 1 + 4 + 1):

• `P[3] - P[0] = 9 - 3 = 6`

Adding 0

In some cases people add a 0 to the beginning of the array

• Simplifies range sum queries: no need for special-case handling when `l = 0`
• Aligns `P[i]` with the sum of the first `i` elements of `A`
• Avoids off-by-one errors in indexing
• Makes the prefix sum array length `n + 1`, which is often more ergonomic in 1-based indexing contexts

This allows fast computation of the sum of any subarray `A[l..r]` using:

• `sum = P[r+1] - P[l]`

Use Cases

• Fast range sum queries
• Histogram equalization
• Cumulative frequency tables
• Sliding window optimizations

Notes

• Can be extended to 2D arrays for matrix prefix sums
• Useful in competitive programming and data preprocessing

Two Pointer Pattern

Purpose

Optimize traversal of arrays or linked lists by using two indices (pointers) to reduce time complexity, often from O(n²) to O(n). The real life example was you’re processing a sorted audit log of user login timestamps. You want to detect if any user has logged in twice within a 5-minute window. Spent a bit of time understanding the O(n²) thing. As the formula for doing the search manually was - n × (n - 1) / 2. The -1 and /2 are ignored to make n². This would be better written for me a n x 0.5(n-1). It is far more easy to see that the 0.5 will influence the outcome but we are still dealing with a parabola (quadratic)

Concept

Use two pointers to scan or compare elements in a sequence:

• Left and Right: Often used for searching or shrinking a window.
• Fast and Slow: Used for cycle detection or distance-based logic.

Typical setup:

• Initialize two pointers (`i`, `j`) at different positions.
• Move one or both based on problem constraints.
• Avoid nested loops by leveraging sorted input or monotonic properties.

Common Use Cases

• Finding pairs with a target sum in a sorted array
• Removing duplicates in-place
• Merging sorted arrays
• Sliding window optimizations
• Cycle detection in linked lists (Floyd’s algorithm)

Example: Pair Sum in Sorted Array

This example is where you are looking for a value say 5 in a sorted array e.g. 0,1,3,5,11,12.

function hasPairWithSum(arr, target) {
  let left = 0;
  let right = arr.length - 1;

  while (left < right) {
    const sum = arr[left] + arr[right];
    if (sum === target) return true;
    if (sum < target) left++;
    else right--;
  }

  return false;
}

Implementation (Rust)

Just for a laugh

fn has_pair_with_sum(sorted: &[i32], target: i32) -> bool {
    let (mut left, mut right) = (0, sorted.len() - 1);

    while left < right {
        let sum = sorted[left] + sorted[right];
        if sum == target {
            return true;
        } else if sum < target {
            left += 1;
        } else {
            right -= 1;
        }
    }

    false
}

fn main() {
    let nums = vec![1, 2, 4, 7, 11, 15];
    let target = 15;

    if has_pair_with_sum(&nums, target) {
        println!("Found a pair that sums to {}", target);
    } else {
        println!("No pair found");
    }
}

Why It Works

• Sorted input allows directional decisions (increase left or decrease right).
• Avoids brute-force O(n²) pair checking.
• Efficient for problems with monotonic constraints.

Variants

Pattern	Use Case	Movement Logic
Left–Right	Sorted array pair sum	Move inward based on sum
Fast–Slow	Cycle detection	Fast moves 2x, slow moves 1x
Sliding Window	Max sum subarray	Expand/shrink window based on condition

Speed Comparison

This table compares the brute-force and two-pointer approaches for finding a pair of numbers that sum to a target in a sorted array.

Method	Description	Time Complexity	Checks for n = 5	Checks for n = 100	Checks for n = 1,000
Brute-force	Try every possible pair using nested loops	O(n²)	10	4,950	499,500
Two-pointer	Start at both ends, move inward based on sum comparison	O(n)	≤ 4	≤ 99	≤ 999

Notes

• Often paired with prefix sums or hash maps for hybrid strategies
• Works best when input is sorted or has predictable structure

Sliding Window Pattern

Purpose

Efficiently process contiguous subarrays or substrings by maintaining a moving window of elements. Reduces time complexity from O(n²) to O(n) in many cases. Gosh the robot does put it in bizarre words for me. This is when you are asked the highest value sub array e.g. given an array 5,2,4,3,-1,9,3,7,6. What is the maximum value for 4 elements. To reduce the traversal of the array for each window we remove the element on the left leaving the window and add the element on the right entering the window.

Concept

Use two pointers (`start`, `end`) to define a window over a sequence:

• Expand the window by moving `end` forward.
• Shrink the window by moving `start` forward when constraints are violated.
• Track metrics (sum, length, frequency) within the window.

Common Use Cases

• Maximum sum of k-length subarray
• Longest substring without repeating characters
• Minimum window that satisfies a condition
• Real-time stream processing (e.g., rolling averages)

Example: Max Sum of Subarray of Size k

fn max_sum_subarray(arr: &[i32], k: usize) -> i32 {
    if arr.len() < k { return 0; }

    let mut max_sum = 0;
    let mut window_sum = arr[..k].iter().sum();

    max_sum = window_sum;

    for i in k..arr.len() {
        window_sum += arr[i] - arr[i - k];
        max_sum = max_sum.max(window_sum);
    }

    max_sum
}

Why It Works

• Avoids recomputing sums from scratch
• Maintains a fixed-size or dynamic window
• Efficient for problems involving contiguous elements

Variants

Variant	Use Case	Window Behavior
Fixed-size	Max sum of k-length subarray	Window slides forward by 1
Dynamic-size	Longest substring without repeats	Expand/shrink based on condition
Frequency-based	Minimum window with all chars	Track counts in a hashmap

Notes

• Often combined with hash maps or frequency counters
• Works best on arrays, strings, or streams
• Can be extended to 2D grids or time-based windows

Related Patterns

• Prefix Sum: for cumulative metrics
• Two Pointer: for sorted arrays or pair comparisons
• Monotonic Queue: for sliding window max/min with order constraints

Fast and Slow Pointer Pattern

Purpose

Efficiently traverse sequences (arrays, linked lists, streams) using two pointers moving at different speeds. Commonly used for:

• Cycle detection
• Finding the middle of a list
• Detecting duplicates or convergence
• Space-efficient traversal

The important bit for me was the word cycle. It means when a node points to back to another node. This appears to be a common thing to detect.

Concept

Use two pointers:

• `slow` moves one step at a time
• `fast` moves two steps at a time

General Algorithm

1. Initialize slow = 0, fast = 0
2. While fast and fast.next exist:
   a. slow = slow.next
   b. fast = fast.next.next
3. If slow == fast → cycle detected

Example: Cycle Detection in Linked List

As mentions above, this is detecting when one node, points to a previous.

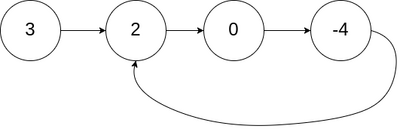
fn has_cycle(head: &Option<Box<ListNode>>) -> bool {
    let mut slow = head.as_ref();
    let mut fast = head.as_ref();

    while let (Some(s), Some(f)) = (slow, fast.and_then(|f| f.next.as_ref())) {
        slow = s.next.as_ref();
        fast = f.next.as_ref();
        if std::ptr::eq(slow, fast) {
            return true;
        }
    }

    false
}

Example: Finding Middle of Linked List

The example which made the most sense was a LRU (Least Recently Used) cache. You look for the middle to dump the oldest.

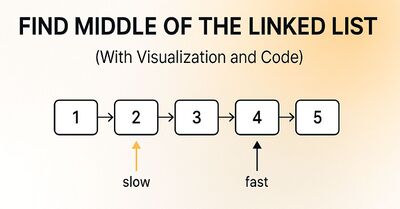
ListNode findMiddle(ListNode head) {
    ListNode slow = head, fast = head;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow; // Middle node
}

Time and Space Complexity

Operation	Time Complexity	Space Complexity
Cycle detection	O(n)	O(1)
Find middle	O(n)	O(1)
Detect convergence	O(n)	O(1)

Related Patterns

• Sliding Window: for subarray/substring processing
• Two Pointer: for sorted arrays and pair comparisons
• Floyd’s Tortoise and Hare: formal name for cycle detection variant

Notes

• Works best on linked lists or sequences with implicit structure
• Avoids extra memory allocation
• Can be extended to detect loop entry point

See Also

• Sliding Window Pattern
• Prefix Sum Technique
• Two Pointer Strategy

In-Place Reversal Pattern

Purpose

Reverse the order of elements in a sequence (array, string, linked list) without using extra space. This pattern is used for:

• Memory-efficient transformations
• Buffer cleanup or reordering
• Palindrome checks
• Undo operations

Couldn't really find an example except for reversing byte buffer.

Concept

Use two pointers to swap elements from both ends toward the center:

• `left = 0`, `right = n - 1`
• While `left < right`, swap `A[left]` and `A[right]`, then move inward

General Algorithm

1. Initialize left = 0, right = n - 1
2. While left < right:
   a. Swap A[left] and A[right]
   b. Increment left, decrement right

Example: Reverse Array In-Place

fn reverse_in_place(arr: &mut [i32]) {
    let mut left = 0;
    let mut right = arr.len().saturating_sub(1);

    while left < right {
        arr.swap(left, right);
        left += 1;
        right -= 1;
    }
}

Example: Reverse String In-Place (Rust)

fn reverse_string(s: &mut Vec<char>) {
    let mut left = 0;
    let mut right = s.len().saturating_sub(1);

    while left < right {
        s.swap(left, right);
        left += 1;
        right -= 1;
    }
}

Example: Reverse String In-Place (C#)

public static void ReverseInPlace(byte[] buffer)
{
    int left = 0;
    int right = buffer.Length - 1;

    while (left < right)
    {
        byte temp = buffer[left];
        buffer[left] = buffer[right];
        buffer[right] = temp;

        left++;
        right--;
    }
}

byte[] payload = new byte[] { 1, 2, 3, 4, 5 };
ReverseInPlace(payload);
// payload is now { 5, 4, 3, 2, 1 }

Example: Carousel

Finally a use case I can understand. A carousel is a blog of posts maybe and you want them in descending order.

// components/InPlaceCarousel.tsx
import React from "react";

interface CarouselProps {
  items: string[];
  reversed?: boolean;
}

function reverseInPlace<T>(arr: T[]): void {
  let left = 0;
  let right = arr.length - 1;

  while (left < right) {
    [arr[left], arr[right]] = [arr[right], arr[left]];
    left++;
    right--;
  }
}

export const InPlaceCarousel: React.FC<CarouselProps> = ({ items, reversed = false }) => {
  const displayItems = [...items]; // clone to avoid mutating props

  if (reversed) {
    reverseInPlace(displayItems); // mutate the clone
  }

  return (
    <div className="flex overflow-x-auto space-x-4 p-4">
      {displayItems.map((item, index) => (
        <div
          key={index}
          className="min-w-[200px] h-[120px] bg-gray-100 rounded-md flex items-center justify-center shadow-md"
        >
          {item}
        </div>
      ))}
    </div>
  );
};

And usage

// pages/index.tsx
import { InPlaceCarousel } from "@/components/InPlaceCarousel";

export default function Home() {
  const items = ["Alpha", "Beta", "Gamma", "Delta"];

  return (
    <main className="p-8">
      <h2 className="text-xl font-bold mb-4">Normal Order</h2>
      <InPlaceCarousel items={items} />

      <h2 className="text-xl font-bold mt-8 mb-4">Reversed In-Place</h2>
      <InPlaceCarousel items={items} reversed />
    </main>
  );
}

Time and Space Complexity

Operation	Time Complexity	Space Complexity
Array reversal	O(n)	O(1)
String reversal	O(n)	O(1)
Linked list reversal	O(n)	O(1)

Use Cases

• Reversing buffers or byte streams
• Palindrome validation
• Undoing transformations
• Reversing singly linked lists (with pointer rewiring)
• UI animations (e.g., reversing carousel order)

Related Patterns

• Two Pointer Pattern: used to drive the reversal
• Fast and Slow Pointer: for midpoint detection before reversal
• Stack-based reversal: alternative using extra space

Notes

• Works best on mutable sequences
• For linked lists, requires pointer rewiring instead of index swapping
• Can be extended to reverse subarrays or segments

Monotonic Stack Pattern

Purpose

Maintain a stack that is either strictly increasing or decreasing to efficiently solve problems involving:

• Next Greater Element (NGE)
• Next Smaller Element (NSE)
• Span problems (e.g., stock span)
• Histogram area calculations

This was a bit tricky for me. The goal is to not do a calculation for everything in the array. So is we had a height of a histogram held in an array e.g. [2, 1, 5, 6, 2, 3, 0]. Every time you pop an element, you calculate the area for the element popped. For brute force this may be ~36 calculations with monotonic ~18

Step	Index (i)	Height h[i]	Stack Before	Action	Area Computed	Stack After
0	0	2	[]	Push 0	—	[0]
1	1	1	[0]	Pop 0 (height=2, width=1)	2 × 1 = 2	[]
			[]	Push 1	—	[1]
2	2	5	[1]	Push 2	—	[1, 2]
3	3	6	[1, 2]	Push 3	—	[1, 2, 3]
4	4	2	[1, 2, 3]	Pop 3 (height=6, width=1)	6 × 1 = 6	[1, 2]
			[1, 2]	Pop 2 (height=5, width=2)	5 × 2 = 10	[1]
			[1]	Push 4	—	[1, 4]
5	5	3	[1, 4]	Push 5	—	[1, 4, 5]
6	6	0	[1, 4, 5]	Pop 5 (height=3, width=1)	3 × 1 = 3	[1, 4]
			[1, 4]	Pop 4 (height=2, width=4)	2 × 4 = 8	[1]
			[1]	Pop 1 (height=1, width=6)	1 × 6 = 6	[]
			[]	Push 6	—	[6]

Concept

Use a stack to track indices or values while enforcing a monotonic order:

• **Increasing stack**: top is smallest, used for next smaller elements
• **Decreasing stack**: top is largest, used for next greater elements

General Algorithm

1. Initialize empty stack
2. Iterate over array:
   a. While stack is not empty and current violates monotonicity:
      - Pop from stack
   b. Push current index/value onto stack

Example: Next Greater Element

public int[] NextGreaterElements(int[] nums) {
    int n = nums.Length;
    int[] result = new int[n];
    Stack<int> stack = new();

    for (int i = n - 1; i >= 0; i--) {
        while (stack.Count > 0 && stack.Peek() <= nums[i]) {
            stack.Pop();
        }

        result[i] = stack.Count == 0 ? -1 : stack.Peek();
        stack.Push(nums[i]);
    }

    return result;
}

Time and Space Complexity

Operation	Time Complexity	Space Complexity
Next Greater/Smaller Element	O(n)	O(n)
Histogram Area	O(n)	O(n)

Use Cases

• Finding next greater/smaller elements
• Calculating largest rectangle in histogram
• Stock span problems
• Sliding window optimizations
• Rainwater trapping (with two-pointer variant)

Related Patterns

• Two Pointer Pattern: often used alongside for bidirectional sweeps
• In-Place Reversal: used in post-processing results
• Prefix Sum: complements monotonic stack in histogram or span problems

Notes

• Stack stores indices for flexibility
• Can be adapted for circular arrays (modulo indexing)
• Useful in both frontend (layout calculations) and backend (data stream analysis)

Top K Elements

Purpose

Efficiently retrieve the k largest elements from a dataset, typically for ranking, filtering, or prioritization. This is foundational in analytics, search, and real-time systems. This does seem to be something I might want to do. Many of these I have not really come across in 40 years of doing this. I do not work, in general, in analysis or graphics. So here goes.

Concept

Maintain a dynamic structure (usually a min-heap of size k) that tracks the top k values as the array is processed. This avoids sorting the entire array and reduces time complexity when k ≪ n.

Common Use Cases

• Ranking top scores or metrics
• Search engines: top relevant results
• Real-time dashboards: top trending items
• Log analysis: top error types or sources

Example (Typescript)

To find the to K Elements you can put the elements in a MinHeap. There are two types of these Min and Max.

To find the largest we use the minHeap and for the smallest the maxHeap (not shown)

class MinHeap {
  private heap: number[] = [];

  size(): number {
    return this.heap.length;
  }

  peek(): number | undefined {
    return this.heap[0];
  }

  push(val: number): void {
    this.heap.push(val);
    this.bubbleUp();
  }

  pop(): number | undefined {
    if (this.heap.length === 0) return undefined;
    const top = this.heap[0];
    const end = this.heap.pop()!;
    if (this.heap.length > 0) {
      this.heap[0] = end;
      this.bubbleDown();
    }
    return top;
  }

  private bubbleUp(): void {
    let idx = this.heap.length - 1;
    const element = this.heap[idx];
    while (idx > 0) {
      const parentIdx = Math.floor((idx - 1) / 2);
      const parent = this.heap[parentIdx];
      if (element >= parent) break;
      this.heap[idx] = parent;
      this.heap[parentIdx] = element;
      idx = parentIdx;
    }
  }

  private bubbleDown(): void {
    let idx = 0;
    const length = this.heap.length;
    const element = this.heap[0];
    while (true) {
      let leftIdx = 2 * idx + 1;
      let rightIdx = 2 * idx + 2;
      let swapIdx: number | null = null;

      if (leftIdx < length) {
        if (this.heap[leftIdx] < element) swapIdx = leftIdx;
      }

      if (rightIdx < length) {
        if (
          (swapIdx === null && this.heap[rightIdx] < element) ||
          (swapIdx !== null && this.heap[rightIdx] < this.heap[leftIdx])
        ) {
          swapIdx = rightIdx;
        }
      }

      if (swapIdx === null) break;
      this.heap[idx] = this.heap[swapIdx];
      this.heap[swapIdx] = element;
      idx = swapIdx;
    }
  }

  toSortedArray(): number[] {
    const copy = [...this.heap];
    const result: number[] = [];
    while (this.size() > 0) {
      result.push(this.pop()!);
    }
    this.heap = copy;
    return result.reverse(); // largest to smallest
  }
}

function topKElements(nums: number[], k: number): number[] {
  const heap = new MinHeap();

  for (const num of nums) {
    if (heap.size() < k) {
      heap.push(num);
    } else if (num > heap.peek()!) {
      heap.pop();
      heap.push(num);
    }
  }

  return heap.toSortedArray();
}

// Example usage:
const nums = [3, 1, 5, 12, 2, 11];
const k = 3;
console.log(topKElements(nums, k)); // Output: [12, 11, 5]

Why It Works

Using a min-heap of size k ensures:

• The smallest of the top k is always at the root
• Any new value greater than the root replaces it
• Heap maintains top k values in O(n log k) time

This avoids full sorting (O(n log n)) and is optimal when k is much smaller than n.

Variants

• Top K Frequent Elements (by frequency)
• Top K in Streaming Data (online updates)
• Top K with Ties (handle duplicates)
• Top K by Custom Comparator (e.g., score + timestamp)

Notes

• Use max-heap if you need smallest k elements
• Quickselect is faster for unsorted arrays when order doesn’t matter
• Sorting is simplest but less efficient for large n
• Heap-based approach is ideal for real-time or memory-constrained systems

Overlapping Intervals

Purpose

Detect and merge overlapping intervals in a list of ranges. This pattern is used to:

• Consolidate time blocks or resource allocations
• Detect conflicts in scheduling or bookings
• Normalize ranges for efficient querying

Concept

Sort intervals by start time, then iterate and merge overlapping ones:

• If current interval overlaps with the previous → merge
• Else → add as a new block

Common Use Cases

• Calendar event conflict resolution
• CPU or memory range merging
• Booking system availability
• Firewall rule normalization
• Genomic range analysis

Example: Merge Overlapping Intervals (TypeScript)

type Interval = [number, number];

function mergeIntervals(intervals: Interval[]): Interval[] {
  if (intervals.length === 0) return [];

  // Sort by start time
  intervals.sort((a, b) => a[0] - b[0]);

  const merged: Interval[] = [intervals[0]];

  for (let i = 1; i < intervals.length; i++) {
    const [prevStart, prevEnd] = merged[merged.length - 1];
    const [currStart, currEnd] = intervals[i];

    if (currStart <= prevEnd) {
      // Overlap → merge
      merged[merged.length - 1][1] = Math.max(prevEnd, currEnd);
    } else {
      // No overlap → add new
      merged.push([currStart, currEnd]);
    }
  }

  return merged;
}

// Example usage:
const input: Interval[] = [[1, 3], [2, 6], [8, 10], [9, 12]];
console.log(mergeIntervals(input)); // Output: [[1, 6], [8, 12]]

Why It Works

• Sorting ensures intervals are processed in order
• Overlap is detected by comparing current start with previous end
• Merging is done in-place, preserving minimal space usage
• Guarantees non-overlapping output in O(n log n) time

Variants

• Insert and merge a new interval into existing list
• Count total coverage (union of intervals)
• Detect conflicts without merging
• Interval intersection (e.g., common availability)

Notes

• Sorting is key — without it, merging fails
• Can be adapted to handle open/closed intervals
• Useful in both frontend (calendar UI) and backend (range indexing)
• For large datasets, consider segment trees or interval trees

Binary Search

Purpose

Efficiently locate a target value or decision point in a sorted array or monotonic search space. Reduces time complexity from O(n) to O(log n). Basically you start from the middle and test if the target value is < or > and discard search the other side thus saving time. Rinse and repeat.

Concept

Repeatedly divide the search space in half:

• Compare target with middle element
• Narrow search to left or right half based on comparison
• Stop when target is found or search space is empty

Common Use Cases

• Search for a target in sorted array
• Find first or last occurrence of a value
• Locate insertion point (lower/upper bound)
• Binary search on answer (e.g., min/max feasible value)
• Peak finding in unimodal arrays

Example: Basic Binary Search (TypeScript)

function binarySearch(nums: number[], target: number): number {
  let left = 0, right = nums.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);

    if (nums[mid] === target) return mid;
    else if (nums[mid] < target) left = mid + 1;
    else right = mid - 1;
  }

  return -1; // not found
}

Why It Works

• Sorted input guarantees predictable direction
• Halving search space each step → O(log n) time
• Works on arrays, ranges, or virtual search spaces

Variants

• Lower bound: first index ≥ target
• Upper bound: first index > target
• First/last occurrence with duplicates
• Binary search on answer (e.g., capacity, radius, speed)
• Search in rotated or infinite arrays (see Modified Binary Search)

Notes

• Always validate sorted input before applying
• Watch for overflow in `mid = (left + right) / 2` → use `left + (right - left) / 2`
• Can be adapted to floats, ranges, or custom comparators
• Foundation for many optimization and decision problems

Modified Binary Search

Purpose

Adapt binary search to solve problems where the array is:

• Rotated or partially sorted
• Contains duplicates or gaps
• Requires condition-based search (not exact match)

Used to locate elements, boundaries, or decision points in O(log n) time. For example given

Rotated Arrays

A rotated array is a sorted array that’s been shifted circularly

[1, 2, 3, 4, 5, 6]

After rotating right by 2 positions:

[5, 6, 1, 2, 3, 4]

After rotating left by 2 positions:

[3, 4, 5, 6, 1, 2]

Concept

Standard binary search assumes a fully sorted array. Modified variants:

• Adjust mid-point logic based on structure
• Use conditions to guide search direction
• Often return boundaries (first/last occurrence, peak, etc.)

Common Use Cases

• Search in rotated sorted array
• Find peak element in mountain array
• Locate first/last occurrence of target
• Binary search on answer (e.g., min/max feasible value)
• Search in infinite or unknown-sized array

Example: Search in Rotated Sorted Array (TypeScript)

function searchRotated(nums: number[], target: number): number {
  let left = 0, right = nums.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);

    if (nums[mid] === target) return mid;

    // Left half is sorted
    if (nums[left] <= nums[mid]) {
      if (nums[left] <= target && target < nums[mid]) {
        right = mid - 1;
      } else {
        left = mid + 1;
      }
    }
    // Right half is sorted
    else {
      if (nums[mid] < target && target <= nums[right]) {
        left = mid + 1;
      } else {
        right = mid - 1;
      }
    }
  }

  return -1;
}

Why It Works

• Rotated arrays have one sorted half → use that to guide search
• Mid-point comparison reveals which half is sorted
• Conditions narrow search space while preserving O(log n) time

Variants

• Find minimum in rotated array
• Binary search on answer (e.g., capacity, speed, radius)
• Peak finding in unimodal arrays
• First/last occurrence with duplicates
• Search in infinite array using exponential bounds

Notes

• Always validate which half is sorted before deciding direction
• Watch for edge cases with duplicates (may degrade to O(n))
• Binary search on answer is powerful for optimization problems
• Useful in both algorithmic interviews and backend range queries

Tree Traversal

Traversal Types

There a four of types of key traversal.

Traversal	Order	Data Structure	Analogy	Common Use Cases
Pre-order	Node → Left → Right	Stack (recursion or explicit)	Packing a suitcase: handle current item before sub-items	Serialize tree, prefix expression
In-order	Left → Node → Right	Stack (recursion or explicit)	Reading a book: left page, center binding, right page	BST: sorted order, expression evaluation
Post-order	Left → Right → Node	Stack (recursion or explicit)	Cleaning a room: tidy sub-areas before marking complete	Delete tree, postfix expression
Level-order (BFS)	Top-down, left to right	Queue	Breadth-first: process all nodes at current depth	Shortest path, friend-of-friend expansion

Pre-order

In-order

Post-order

Level-order (BFS)

See below

Depth-First Search (DFS)

Purpose

Explore as deep as possible along each branch before backtracking. DFS is ideal for problems involving exhaustive search, pathfinding with constraints, or recursive structure traversal.

More Visual

For DFS we search done rather than across

A clear picture of searching would be

Concept

Use a stack (explicit or via recursion) to dive deep into each path:

• Start from a source node
• Explore one neighbor fully before moving to the next
• Backtrack when no unvisited neighbors remain

Common Use Cases

• Pathfinding with constraints (e.g., all paths, cycle detection)
• Topological sorting
• Solving puzzles (e.g., Sudoku, N-Queens)
• Tree traversals (preorder, inorder, postorder)
• Backtracking problems (e.g., permutations, combinations)

Example: Cycle Detection in Directed Graph (TypeScript)

function hasCycle(graph: Map<number, number[]>): boolean {
  const visited = new Set<number>();
  const recStack = new Set<number>();

  function dfs(node: number): boolean {
    if (recStack.has(node)) return true;
    if (visited.has(node)) return false;

    visited.add(node);
    recStack.add(node);

    for (const neighbor of graph.get(node) || []) {
      if (dfs(neighbor)) return true;
    }

    recStack.delete(node);
    return false;
  }

  for (const node of graph.keys()) {
    if (dfs(node)) return true;
  }

  return false;
}

Why It Works

• Recursion or stack ensures deep traversal
• Backtracking allows full path exploration
• Recursion stack can track path state (e.g., for cycle detection)
• Efficient for problems with branching decisions

Variants

• Recursive DFS (natural for trees)
• Iterative DFS using a stack
• Post-order DFS for dependency resolution
• DFS with state tracking (e.g., visited + path constraints)

Notes

• Use a stack (or recursion) — depth-first means diving deep
• Track visited nodes to avoid infinite loops
• Ideal for problems where you need to explore **all** possibilities
• Can be adapted to grids, graphs, trees, or implicit state spaces

Breadth-First Search (BFS)

Purpose

Explore nodes or states level by level, starting from a root or source. BFS guarantees the shortest path in unweighted graphs and is ideal for problems involving proximity, reachability, or layered expansion.

More Visual

Basically we search the tree level by level. Here are some terms

And this is a clearer (hopefully) image showing the approach.

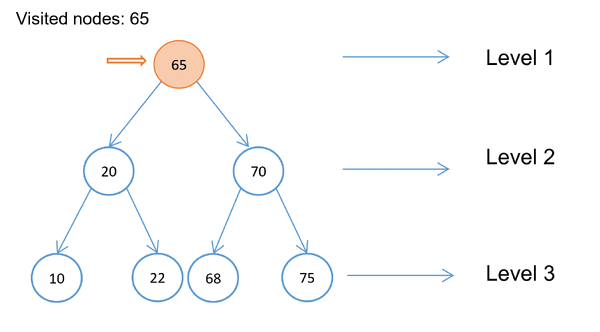
Concept

Use a queue to process nodes in the order they’re discovered:

• Start from a source node
• Visit all immediate neighbors before moving deeper
• Track visited nodes to avoid cycles or redundant work

Common Use Cases

• Shortest path in unweighted graphs
• Level-order traversal of trees
• Finding connected components
• Maze solving (minimum steps)
• Social network expansion (e.g., friend-of-friend)

Example: Shortest Path in Unweighted Graph (TypeScript)

function bfsShortestPath(graph: Map<number, number[]>, start: number, target: number): number {
  const visited = new Set<number>();
  const queue: [number, number][] = [[start, 0]]; // [node, distance]

  while (queue.length > 0) {
    // Remove and return first in queue
    const [node, dist] = queue.shift()!;

    // If node == target return
    if (node === target) return dist;

    // If node already exists continue
    if (visited.has(node)) continue;

    // Else add Node
    visited.add(node);

    // Iterate over neighbours and push onto queue (visited)
    for (const neighbours of graph.get(node) || []) {
      queue.push([neighbor, dist + 1]);
    }
  }

  return -1; // target not reachable
}

Why It Works

• Queue ensures nodes are processed in order of discovery
• Guarantees shortest path in unweighted graphs
• Avoids revisiting nodes via a visited set
• Naturally fits problems with layered or radial expansion

Variants

• Level-order traversal in binary trees
• Multi-source BFS (e.g., fire spread from multiple points)
• Bidirectional BFS (search from both ends)
• BFS with state tracking (e.g., grid + keys collected)

Notes

• Use a queue, not a stack — order matters
• Track visited nodes to prevent infinite loops
• For weighted graphs, use Dijkstra’s algorithm instead
• Can be adapted to grids, trees, graphs, or even implicit state spaces

BFS vs DFS Comparison

Feature	Breadth-First Search (BFS)	Depth-First Search (DFS)
Traversal Order	Level by level	Deep into one branch before backtracking
Data Structure	Queue (FIFO)	Stack (explicit or via recursion)
Use Case Example	Find shortest path in an unweighted graph	Detect cycles or explore all paths
Real-World Analogy	Ripples from a stone in a pond	Maze solving by going as far as possible before turning back
Guarantees Shortest Path?	✅ Yes (in unweighted graphs)	❌ No
Memory Usage	Can be high (stores all nodes at current level)	Often lower (stores one path at a time)
Common Problems	Level-order traversal, shortest path, friend-of-friend expansion	Topological sort, cycle detection, puzzle solving
Grid Traversal Behavior	Expands outward evenly	Dives deep into one direction
Recursive?	Rarely (usually iterative with queue)	Often recursive
Suitable For Large Graphs?	Yes, if depth is shallow	Yes, if depth is manageable
Example Question	"Find the shortest path from A to B in a maze"	"Find all paths from A to B in a maze"
Failure Mode	Can consume lots of memory if graph is wide	Can hit recursion limits if graph is deep

Matrix Traversal

Purpose

Efficiently explore or process elements in a 2D grid — for pathfinding, region labeling, flood fill, or dynamic programming.

Concept

• Treat the matrix as a graph: each cell is a node, and adjacent cells are edges.
• Use direction vectors to move in 4 or 8 directions.
• Track visited cells to avoid revisiting.
• BFS for shortest path; DFS for region exploration.

Implementation (C# Template)

int[,] grid = {
    {1, 1, 0},
    {0, 1, 0},
    {1, 0, 1}
};

int rows = grid.GetLength(0);
int cols = grid.GetLength(1);
bool[,] visited = new bool[rows, cols];

int[] dx = {-1, 1, 0, 0}; // Up, Down
int[] dy = {0, 0, -1, 1}; // Left, Right

void DFS(int x, int y) {
    if (x < 0 || x >= rows || y < 0 || y >= cols || visited[x, y] || grid[x, y] == 0)
        return;

    visited[x, y] = true;

    for (int d = 0; d < 4; d++) {
        DFS(x + dx[d], y + dy[d]);
    }
}

Example

Count connected regions of 1s (islands):

int count = 0;
for (int i = 0; i < rows; i++) {
    for (int j = 0; j < cols; j++) {
        if (!visited[i, j] && grid[i, j] == 1) {
            DFS(i, j);
            count++;
        }
    }
}
Console.WriteLine($"Island count: {count}");

Adding 0

- Padding: Add a border of 0s around the matrix to simplify edge checks. - Marking visited: Set visited cells to 0 if mutation is allowed (e.g., grid[x, y] = 0). - Zero-fill: Used in DP tables or initialization.

Use Cases

- Flood fill (e.g., coloring regions) - Count islands / regions - Shortest path in grid (BFS) - Spiral or zigzag printing - DP table fill (e.g., edit distance, path count)

Notes

- Always check bounds: x >= 0 && x < rows, y >= 0 && y < cols - Use visited[,] if mutation isn’t allowed - BFS uses a Queue<(int x, int y)> in C# - For 8-directional traversal, expand dx/dy arrays - Spiral traversal requires careful bound updates

Backtracking

Purpose

Explore all possible configurations of a problem by incrementally building candidates and abandoning paths that violate constraints. Ideal for puzzles, combinatorics, and constraint satisfaction.

My Take

So I guess the first thing I think of for this a maze. Given this, this made lots of sense for development. e.g. maps between too points. Love recursion too. So here goes. I guess I will choose C++ today.

Example 1 DFS

I liked this solution because the model was very easy on the eye to understand.

#include <iostream>

const int ROWS = 10;
const int COLS = 10;

char maze[ROWS][COLS] = {
    {'#', '#', '#', '#', '#', '#', '#', '#', '#', '#'},
    {'#', 'S', '.', '.', '#', '.', '.', '.', '.', '#'},
    {'#', '#', '#', '.', '#', '.', '#', '#', '.', '#'},
    {'#', '.', '.', '.', '.', '.', '.', '#', '.', '#'},
    {'#', '.', '#', '#', '#', '#', '.', '#', '.', '#'},
    {'#', '.', '.', '.', '.', '#', '.', '#', '.', '#'},
    {'#', '#', '#', '#', '.', '#', '.', '#', '.', '#'},
    {'#', '.', '.', '#', '.', '#', '.', '#', '.', '#'},
    {'#', '.', '#', '#', '.', '#', '.', '.', 'G', '#'},
    {'#', '#', '#', '#', '#', '#', '#', '#', '#', '#'}
};

bool visited[ROWS][COLS] = {false};

bool dfs(int x, int y) {
    
    // Bounds check
    if (x < 0 || y < 0 || x >= ROWS || y >= COLS) return false;

    // Wall or visited
    if (maze[x][y] == '#' || visited[x][y]) return false;

    // Goal found
    if (maze[x][y] == 'G') {
        std::cout << "Reached goal at (" << x << "," << y << ")\n";
        return true;
    }

    // Mark as visited
    visited[x][y] = true;

    // Optional: mark path
    if (maze[x][y] == '.') maze[x][y] = 'v';

    // Explore in 4 directions
    if (dfs(x + 1, y)) return true;
    if (dfs(x - 1, y)) return true;
    if (dfs(x, y + 1)) return true;
    if (dfs(x, y - 1)) return true;

    // Optional: unmark if backtracking
    // maze[x][y] = '.';

    return false;
}

int main() {
    // Find start position
    for (int i = 0; i < ROWS; i++) {
        for (int j = 0; j < COLS; j++) {
            if (maze[i][j] == 'S') {
                if (dfs(i, j)) {
                    std::cout << "Path found!\n";
                } else {
                    std::cout << "No path to goal.\n";
                }
            }
        }
    }

    // Print maze with path
    for (int i = 0; i < ROWS; i++) {
        for (int j = 0; j < COLS; j++) {
            std::cout << maze[i][j] << ' ';
        }
        std::cout << '\n';
    }

    return 0;
}

Example 2 DFS

In this one we model the maze by stating which points are accessible. This was a lot hard on the eye for the same challenge.

bool visited2[100] = {false};
std::list<int> maze2[100];

void buildMaze() {
    // Example corridor from node 11 to 93
    maze2[11].push_back(12);
    maze2[12].push_back(13);
    maze2[13].push_back(23);
    maze2[23].push_back(33);
    maze2[33].push_back(43);
    maze2[43].push_back(53);
    maze2[53].push_back(63);
    maze2[63].push_back(73);
    maze2[73].push_back(83);
    maze2[83].push_back(93); // Goal

    maze2[12].push_back(11);
    maze2[13].push_back(12);
    maze2[23].push_back(13);
    maze2[33].push_back(23);
    maze2[43].push_back(33);
    maze2[53].push_back(43);
    maze2[63].push_back(53);
    maze2[73].push_back(63);
    maze2[83].push_back(73);
    maze2[93].push_back(83);

    maze2[13].push_back(14);
    maze2[14].push_back(13);

    maze2[33].push_back(34);
    maze2[34].push_back(35);
    maze2[35].push_back(36);
    maze2[36].push_back(37);

    maze2[34].push_back(33);
    maze2[35].push_back(34);
    maze2[36].push_back(35);
    maze2[37].push_back(36);

    // Loop back path
    maze2[53].push_back(54);
    maze2[54].push_back(55);
    maze2[55].push_back(65);
    maze2[65].push_back(63);

    maze2[54].push_back(53);
    maze2[55].push_back(54);
    maze2[65].push_back(55);
    maze2[63].push_back(65);
}

bool dfs2(int current, int goal) {
    if (current == goal) {
        std::cout << "Reached goal: " << goal << "\n";
        return true;
    }

    visited2[current] = true;

    for (int neighbor : maze2[current]) {
        if (!visited2[neighbor]) {
            if (dfs2(neighbor, goal)) return true;
        }
    }

    return false;
}

int main() {
    buildMaze();

    int start = 11;
    int goal = 93;

    if (dfs2(start, goal)) {
        std::cout << "Path found!\n";
    } else {
        std::cout << "No path to goal.\n";
    }

    return 0;
}

Concept

• Recursively build a solution one step at a time.
• At each step, check if the current state is valid.
• If invalid → backtrack (undo last step).
• If valid → continue exploring deeper.

Implementation (C# Template)

void Backtrack(List<int> path, int start, int n, int k) {
    if (path.Count == k) {
        Console.WriteLine(string.Join(",", path));
        return;
    }

    for (int i = start; i <= n; i++) {
        path.Add(i);
        Backtrack(path, i + 1, n, k);
        path.RemoveAt(path.Count - 1); // backtrack
    }
}

Example

Generate all combinations of 3 numbers from 1 to 5:

Backtrack(new List<int>(), 1, 5, 3);
// Output:
// 1,2,3
// 1,2,4
// ...

Adding 0

• Used to **mark visited cells** in grid-based problems (e.g., Sudoku, maze).
• Can represent **invalid or blocked states**.
• Helps prune paths early — avoids unnecessary recursion.

Use Cases

• Sudoku solver
• N-Queens problem
• Word search in grid
• Subset and permutation generation
• Maze solving with constraints

Notes

• Backtracking is DFS with undo.
• Pruning early improves performance.
• Use visited flags or mutation to track state.
• Can be combined with memoization for optimization.

DP (Dynamic Programming) Patterns

• Fibonacci Numbers
• 0/1 Knapsack
• Longest Common Subsequence (LCS)
• Longest Increasing Subsequence (LIS)
• Subset Sum
• Matrix Chain Multiplication

Fibonacci Numbers

This when you use the two previous numbers to calculate the next. For me it always reminds me of recursion and stack overflow.

0 + 1 = 1 (The sequence is now 0, 1, 1) 
1 + 1 = 2 (The sequence is now 0, 1, 1, 2) 
1 + 2 = 3 (The sequence is now 0, 1, 1, 2, 3) 
2 + 3 = 5 (The sequence is now 0, 1, 1, 2, 3, 5

• Use when: You need to compute a value based on the sum of two previous values.
• Cue: “Nth value depends on (N-1) and (N-2)” — classic linear recurrence.
• Example: Climbing stairs with 1 or 2 steps at a time. You’re at the bottom of a staircase with `n` steps. You can climb either 1 or 2 steps at a time. How many distinct ways are there to reach the top?

Climbing Stairs

As ever with me it is about visualizing the problem. The problem says you can climb the stair with one step or two. So if there were two stairs you could either climb a) using two stairs or b) using climbing one at a time. So the answer is two. To visualize and expand this we can use a decision tree where the choices on each branch is either one step or two step

So here is the full tree for 5 stairs.

Next when looking at this we can see that the decision tree contains many duplicates and therefore wasted processing

So this introduced the Bottom up Dynamic Programming where we take the longest leaf and work backwards to get the answer. If we look a when we are on 5 there is one way to get to five i.e. we are there. Putting yourself of four shows there is still only one way to get to 5. This is always the case. Now is the interesting bit. When you are on three. The options for getting to five are 4 and 5 which we already know, 4=1 5=1 so add them together - bingo Fibonacci

So now the code.

class Solution: 
    def climb(self, n: int) -> int:
        one, two = 1, 1

        // Four boxes to calculate as we already have two of them.
        for i in range(2, n + 1):
            // Calculate next value by adding together
            current = one + two
            two = one
            one = current

        return one

if __name__ == "__main__":
    solution = Solution()
    print(solution.climb(5))

Answer is 8

0/1 Knapsack

• Use when: You must choose items with weights and values, and can't split them.
• Cue: “Maximize value within a fixed capacity” — each item is either taken or skipped.
• Example: Packing a bag with limited space and indivisible items.

Gosh these are all so so long winded. Here is the knapsack one from leetcode.
So the example they gave was how many combinations are there to get 5 with three coins 1,2,5. They draw a table with amounts and coins. For the amount 0 there is only one way to achieve this so 1 is put in that column. The filled on table looks like this.

To calculate the squares add a) you look to the right across the x-axis n squares where n is the coin you are on

And b) add the value directly below to it.

from pyparsing import List

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        cache = {}  # Memoization cache to avoid recomputation

        def dfs(i, a):
            # Base case: exact match — one valid combination
            if a == amount:
                return 1

            # Overshot the amount — invalid path
            if a > amount:
                return 0

            # Ran out of coins — no more options
            if i == len(coins):
                return 0

            # Check if we've already solved this subproblem
            if (i, a) in cache:
                return cache[(i, a)]

            # Recursive step:
            # Option 1: include coins[i] again (stay at i, increase amount)
            # Option 2: skip coins[i] (move to next coin)
            cache[(i, a)] = dfs(i, a + coins[i]) + dfs(i + 1, a)

            return cache[(i, a)]

        # Start from coin index 0 and amount 0
        return dfs(0, 0)
  
if __name__ == "__main__":
    solution = Solution()
    print(solution.change(5, [1, 2, 5]))  # Expected output: 4

Longest Common Subsequence (LCS)

• Use when: You want to compare two sequences and find shared structure.
• Cue: “Find the longest matching pattern between two strings, not necessarily contiguous.”
• Example: Diff tools, DNA sequence alignment, version control merge logic.

Longest Increasing Subsequence (LIS)

• Use when: You need to find a rising trend inside a sequence.
• Cue: “Find the longest ascending path in a list” — not necessarily consecutive.
• Example: Stock price analysis, resume filtering by skill progression.

Subset Sum

• Use when: You need to check if a subset of numbers adds up to a target.
• Cue: “Can I reach this exact total using any combination of these values?”
• Example: Budget planning, partitioning workloads, cryptographic puzzles.

Matrix Chain Multiplication

• Use when: You want to optimize the order of operations to reduce cost.
• Cue: “Minimize total computation cost by choosing optimal grouping.”
• Example: Query planner optimization, compiler instruction scheduling.

Summary

Here is a quick table

Pattern	Example Question	Core Insight	Real-World Analogy
Prefix Sum	"Given an array, find the sum of elements between indices i and j in constant time."	Precompute cumulative totals to answer range queries fast.	Running total on a spreadsheet column.
Two Pointer Pattern	"Find if any two numbers in a sorted array sum to a target."	Use two indices moving inward to reduce search space.	Scanning a sorted guest list from both ends.
Sliding Window Pattern	"Find the longest substring with at most K distinct characters."	Maintain a moving window to track dynamic subarrays.	Monitoring bandwidth usage over the last 5 minutes.
Fast and Slow Pointer	"Detect if a linked list has a cycle."	Use two pointers at different speeds to detect loops.	Two runners on a circular track — one eventually laps the other.
In-Place Reversal	"Reverse a linked list or array without extra space."	Swap elements directly to conserve memory.	Flipping a pancake stack without using another plate.
Monotonic Stack	"Find the next greater element for each item in an array."	Use a stack that maintains increasing or decreasing order.	Tracking temperature spikes — discard cooler days.
Top K Elements	"Find the K largest numbers in a stream."	Use a heap or priority queue to maintain top values.	Keeping top 10 scores on a leaderboard.
Overlapping Intervals	"Merge overlapping meeting times."	Sort and merge intervals based on start/end.	Scheduling rooms for overlapping bookings.
Binary Search	"Find a target in a sorted array."	Divide and conquer by halving the search space.	Looking up a name in a phone book.
Modified Binary Search	"Find the minimum in a rotated sorted array."	Binary search with logic to handle disrupted order.	Searching a rotated clock face for noon.
Tree Traversal	"Print all nodes in a binary tree in-order."	Visit nodes in a structured sequence.	Walking through a nested folder structure.
DFS (Depth-First Search)	"Find all paths from root to leaf in a tree."	Explore one branch deeply before backtracking.	Maze solving by going as far as possible before turning back.
BFS (Breadth-First Search)	"Find the shortest path in an unweighted graph."	Explore all neighbors level by level.	Ripples spreading from a stone in a pond.
Matrix Traversal	"Search for a value in a 2D grid."	Navigate rows and columns with bounds checks.	Scanning a spreadsheet for a keyword.
Backtracking	"Solve a Sudoku puzzle."	Try, fail, and undo — recursively explore options.	Lock picking by trying combinations and rewinding.
DP Patterns	"Find the minimum cost to climb stairs with variable steps."	Break problems into overlapping subproblems with memoization.	Budgeting monthly expenses by reusing past calculations.