Recursion
Introduction
Want to get done the basics for some of this.
Why
Breaks down large chunks into smaller chunks.
When
You use it when problems contain smaller instances of the same problem. E.g. finding how many combinations there are of n items.
Aspects of Recursion
They all have a
- base case
- recursive case
Base Case
This is where the smallest instance of the case can be solved easily. E.g. For number of combinations when the array is empty.
Recursive Case
This is an instance of the problem that shrink the size of the input toward the base case.
Tail Call Recursion
This is a strange topic and the example stranger to. Often feel I do not speak the same language.
const factorial_non_tail = (n) => {
if(n === 1) return 1
return n * factorial_non_tail(n - 1);
}
const factorial_tail = (n, acc = 1) => {
if(n === 1) return acc
return factorial_tail(n - 1, n * acc);
}
In the first example above the last thing it does is n * factorial_non_tail(n - 1). Which means 5 x something but in the second example the last thing it does is a recursion call. Felt quite chuffed when I found out why - always why. Shown below
Tail recursion is important because it can be optimized by compilers or interpreters through a technique called tail call optimization (TCO) or tail call elimination. In essence, when a function is tail-recursive, the compiler can transform the recursive call into a simple jump instruction, effectively reusing the current stack frame instead of creating a new one for each recursive call.
These do support
| Language | Support Level | Notes |
|---|---|---|
| Scheme | ✅ Guaranteed | Required by spec—recursion is core to control flow |
| Haskell | ✅ Strong | Functional purity encourages tail recursion, often optimized |
| OCaml | ✅ Supported | Optimized by compiler when possible |
| Scala | ✅ With @tailrec |
Compiler enforces tail position with annotation |
| C | ✅ Compiler-dependent | GCC and Clang often optimize tail calls |
| Rust | ⚠️ Limited | No built-in TCO, but manual loop conversion is idiomatic |
| JavaScript | ⚠️ Engine-specific | ES6 spec allows it, but only Safari implements it |
These do not
| Language | Reason Why Not Supported |
|---|---|
| Python | ❌ Explicitly avoided—prefers readability and stack traces |
| Java | ❌ No native TCO—JVM doesn’t optimize tail calls |
| Go | ❌ No TCO—encourages loops over recursion |
| C# | ❌ .NET doesn’t optimize tail calls |
| Ruby | ❌ No TCO—stack grows with recursion |
Examples
Example Find Width and Length for Given Area
Again, another rather pointless test, maybe I am just grumpy but cannot see where I would use this. The approach is interesting but not from a software point of view. If asked to do this I would iterate over the all numbers which return as being a factor, get the y co-ordinate. Anyway enough of my grumbling. The recursion answer is to test if we are passed the max and stop, otherwise, if a factor and w and l are closer.
let best = [area, 1]; // fallback: worst case
const _search = (w) => {
// Stop if passed max
if (w > Math.sqrt(area)) return;
// Check if w is a factor
if (area % w === 0) {
// Calculate the length
const l = area / w;
// Update the best dimensions if needed
if (l >= w) {
// Update the best dimensions if needed
const [bestL, bestW] = best;
// Check if the current pair is more square-like
if (Math.abs(l - w) < Math.abs(bestL - bestW)) {
best = [l, w]; // update best if more square-like
}
}
}
_search(w + 1);
};
_search(1);
return best;
Example Reverse Bits in an Integer
Another fairly silly thing to do. Given an integer 43261596 calculate the value if the bits were reversed.
var reverseBits = function(n) {
const _reverse_bits = (n, bitsLeft = 32, result = 0) => {
// Stop when finished
if (bitsLeft === 0) return result;
// Get last bit
const lastBit = n & 1;
// Shifts all bits in result one place to the left.
// Bitwise ORs the shifted result with lastBit
result = (result << 1) | lastBit;
return _reverse_bits(n >>> 1, bitsLeft - 1, result);
};
return _reverse_bits(n);
};
Example Roman to Decimal
I have never thought how roman numeral work. I just read them. The important things to me was
- to convert you add if next value > current value otherwise subtract, e.g. IV 5-1
- it processing two characters at a time.
const romanToInt = (s) => {
const romanMap = new Map([
["I", 1],
["V", 5],
["X", 10],
["L", 50],
["C", 100],
["D", 500],
["M", 1000],
]);
const _romanToInt = (index = 0) => {
if (index >= s.length) return 0;
const currentVal = romanMap.get(s[index]);
const nextVal = romanMap.get(s[index + 1]);
return (nextVal > currentVal)
? nextVal - currentVal + _romanToInt(index + 2)
: currentVal + _romanToInt(index + 1);
};
return _romanToInt();
};
console.log("Answer:", romanToInt("XIV"));
Example Factorial
const factorial = (n) => {
if(n === 1) return 1
return n * factorial(n-1)
}
Example Palindrome
const palindrome = (str) => {
console.log("calling with",str)
if(str.length === 0) return true
if(str.length === 1) return true
if(str[0] !== str[str.length-1]) return false
return palindrome(str.substr(1, str.length-2))
}
Example Sum
This was a bit of enlightenment for improving speed. Did the sum as you would normally do and you can see on line 3 we slice which means we copy.
const _sum = (numbers, idx) => {
if(numbers.length == 0) return 0
return n + sum(numbers.slice(1))
}
A better approach is to create a sub function which takes an index and therefore no more slices
const sum = (numbers) => {
return _sum(numbers, 0)
}
const _sum = (numbers, idx) => {
if(idx == numbers.length) return 0
return numbers[idx] + _sum(numbers, idx + 1)
}
Example String Reversal
This is where I struggle with recursive. Separating the a) reduce the argument and b) forming the result. It seems very odd to me. Maybe my dyslexic brain is fried
const string_rev = (str) => {
if(str.length === 0 || str.length === 1) return str
const result = string_rev(str.slice(1))
return result + str[0]
}
console.log("Reverse:", string_rev("FRED"))
So this is really
string_rev("RED") + "F"
string_rev("ED") + "R"
string_rev("D") + "E"
string_rev("") + "D"
Example dec2bin
Dividing a number by 2 and concatenating the rem making a binary number
const dec2bin2 = (number) => {
if(number === 0 ) return 0
const quotent = Math.floor(number / 2)
const rem = (number % 2).toString()
const result = dec2bin(quotent)
return result + rem
}
Example Binary Search
find 10 in an array of [-1,0,1,2,3,4,7,9,10,20]. Key thing is in order. Took a while to solve this as I need floor and forgot to put brackets around the calculation - argggghhhhhhhhhh.
const binSearch = (val, numbers, left, right) => {
if(left > right) return -1
console.log("calling with left=%d, right=%d", left,right)
// Calculate the mid-point
const mid_point = Math.floor((left + right) / 2)
// const mid_point = (left+right) /2
console.log("mid_point now:%d", mid_point)
// Check if in middle
if(val === numbers[mid_point]) return mid_point
// Test is val is less than mid_point and search lefside
if(val < numbers[mid_point]) {
return binSearch(val, numbers, left, mid_point-1)
}
return binSearch(val, numbers, mid_point + 1, right)
}
console.log("dec2bin", binSearch(10,[-1,0,1,2,3,4,7,9,10,20], 0, 9))
Example Merge Sort
Kinda insane. This splits and array and for each half split down to two characters, sorts, unwinds so 4 characters, sorts until done

const merge = (array, start, mid, end, side) => {
// console.log("Merging start=%d, mid=%d, end=%d", start, mid, end);
console.log(">>--------------------------------")
console.log(array.slice(start, end + 1));
let i = start;
let j = mid + 1;
let k = 0;
let temp = Array(end - start);
while (i <= mid && j <= end) {
if (array[i] <= array[j]) {
temp[k++] = array[i++];
} else {
temp[k++] = array[j++];
}
}
// Add the rest of the values from left sub-array into the result
while (i <= mid) {
temp[k] = array[i];
k++;
i++;
}
// Add the rest of the values from right sub-array into the result
while (j <= end) {
temp[k] = array[j];
k++;
j++;
}
for (i = start; i <= end; i++) {
data[i] = temp[i - start];
}
console.log(array.slice(start, end + 1));
console.log("<<--------------------------------");
};
const mergeSort = (array, start, end) => {
if (array.length === 0) return [];
if (array.length === 1) return array;
if (start < end) {
const mid = Math.floor((start + end) / 2);
mergeSort(array, start, mid);
mergeSort(array, mid + 1, end);
merge(array, start, mid, end);
}
};
const data = [4, 1, 3, 2, 5, 6];
mergeSort(data, 0, data.length - 1);
console.log("Sorted data", data);
The output from merge looks like this for
input data [4, 1, 3, 2, 5, 6]; >>left --------------------------- [ 4, 1 ] [ 1, 4 ] <<-------------------------------- >>left ----------------------------- [ 1, 4, 3 ] [ 1, 3, 4 ] <<-------------------------------- >>right--------------------------- [ 2, 5 ] [ 2, 5 ] <<-------------------------------- >>right--------------------------- [ 2, 5, 6 ] [ 2, 5, 6 ] <<-------------------------------- >>all----------------------------- [ 1, 3, 4, 2, 5, 6 ] [ 1, 2, 3, 4, 5, 6 ] <<-------------------------------- output [ 1, 2, 3, 4, 5, 6 ]
Example Link List
Yum link lists my favourite. This is another head bender for me. I struggled to understand how link_list.next.next is not null. But got there with some debug.
const linklist_reverse = (linked_list) => {
// We dont process an empty linked list
// Or a linked list not link to anything
if(link_list === null) return link_list
if(linked_list.next === null) {
// We need a node with a next.next pointer
console.log("Base case reached with")
return linked_list
}
console.log("Calling with")
prettyPrintLinkedList(linked_list.next);
const result = linklist_reverse(linked_list.next)
console.log("changing node-----------")
prettyPrintLinkedList(linked_list.next);
console.log("using node-----------")
prettyPrintLinkedList(linked_list);
linked_list.next.next = linked_list
linked_list.next = null
console.log("Returning with")
prettyPrintLinkedList(result);
console.log("------------------------")
return result
}
And here is the debugging
Calling with B -> C -> D -> null Calling with C -> D -> null Calling with D -> null // Base case as we have no linked_list.next.next. 4/ returning D -> null 3/ changing node D -> null with C -> D -> null returning D -> C -> null 2/ changing node C -> null with B -> C -> null returning D -> C -> B -> null 1/ changing node B -> null with A -> B -> null returning D -> C -> B -> A -> null
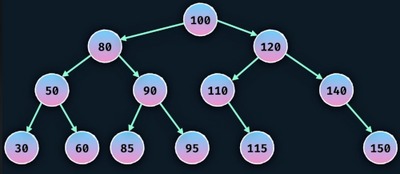
Example Binary Search Tree Insert
The great thing about a bst is you do not need to move nodes to do and insert. Only identify the node it belongs to. And now the robot will build and pretty print it.
- left value must be less than the parent
- right value must be greater than the parent
const binary_search_insert = (bst, value) => {
if (bst === null) {
bst = { value, left: null, right: null };
return bst;
}
if (value < bst.value) {
bst.left = binary_search_insert(bst.left, value);
return bst;
} else {
bst.right = binary_search_insert(bst.right, value);
return bst;
}
};
Example DFS Depth First Search
This is where we traverse a graph going downwards first.

This particular diagram confused a dyslexic like me. So I redrew it
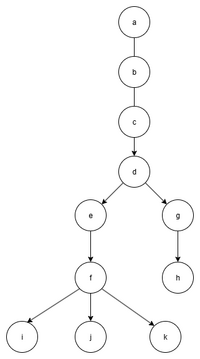
Now here is the structure
const newNodes = {
a: ["b"],
b: ["a", "c"],
c: ["b", "d"],
d: ["c", "e", "g"],
e: ["d", "f"],
f: ["e", "i", "k"],
g: ["d", "h"],
h: ["g"],
i: ["f"],
j: ["f"],
k: ["f"],
};
Finally the dfs search.
const dfs_search = (nodes, current, goal, visited = new Set()) => {
const adjacentNodes = nodes[current];
console.log("Comparing %s with %s", current, goal);
// Base Case: Not Search so false
if (current === null) return false;
// Base Case: Found the goal return true
if (current === goal) return true;
// Iterate over current values
for (let thisNode of adjacentNodes) {
// Already been to this node skip
if (visited.has(thisNode)) continue;
// Not visited, mark as visited
visited.add(thisNode);
const found = dfs_search(nodes, thisNode, goal, visited);
if (found) return true;
}
return false;
};
More Fib
With Fib we use two calls to the same function. This is known as multi branch recursion.
const fib = (n) => {
if(n < 0) return 0
if(n <= 1) return 1
if(n === 2) return 1
return fib(n-1) + fib(n-2)
}
Climbing Stairs (Recursion)
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Still trying to connect pictures with questions. So here goes for climb stairs. First a picture for climb stairs where there are 4 stairs. The successful paths (leaf nodes) in green

In the yellow square, the two child nodes, the left +1 step away, and the right +2 steps away. When you see a binary tree, and the children are k+1 and k+2 then you can use Fibonacci f(n) = f(n-1) + f(n-2) to calculate the number of leaf nodes
Combinations
Common questions are
- Given N things, in how many ways can we arrange them
- In how many ways can we do X
- What is the shortest way to do Y
What is a combination
It is a collection of things where the order does not matter. Important is give [a,b] in a combination it is the same as [b,a]. Given a set of n things, there are 2^n possible combinations.
Example
Looking at [a,b,c] this gives the following

To at each level, the left is if you don't take the level value. So at level a on the left branch we take the parent ([]), on the right we take the level value (a).
Climb Stair with LeetCode
I kept gettting, Time Limit Exceeded. I thought this was the speed I solve the puzzles but it was the execution this. In the leetCode site it was sensitive for memo optimization which meant you create the mem once.
var climbStairs = function(n) {
const mem = {};
function helper(k) {
if (k < 0) return 0;
if (k <= 1) return 1;
if (mem[k]) return mem[k];
mem[k] = helper(k - 1) + helper(k - 2);
return mem[k];
}
return helper(n);
};