Sorting in Code

Selection Sort

Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python

def selection_sort(array):
    m = len(array)
    for i in range(m - 1):
        # Assume the current index (i) has the minimum value
        min_index = i
        # Find the minimum element in the remaining unsorted part
        for j in range(i + 1, m):
            if array[j] < array[min_index]:
                min_index = j
        # Swap the found minimum element with the first element of the unsorted part
        array[i], array[min_index] = array[min_index], array[i]

Looking at the code there are two for loops meaning this is O(n²)
And here it is in rust

fn selection_sort(numbers: &mut Vec<i32>) {
    for i in 0..numbers.len() {
        let mut min_index = i;
        for j in i..numbers.len() {
            if numbers[j] < numbers[min_index] {
                min_index = j;
            }
        }
        numbers.swap(i, min_index);
    }
}

Bubble Sort

This was the first sort I did 40 years ago. Here in rust. Again this is this is O(n²)

fn bubble_sort(numbers: &mut Vec<i32>) {
    for i in 0..numbers.len() {
        for j in 0..numbers.len() - 1 {
            if numbers[j] > numbers[j + 1] {
                numbers.swap(j, j + 1);
            }
        }
    }
}

There were improvements made in the course to the original answer where they identified code repeated even thought we knew the data was already sorted. A clear reason not to just cut and paste.

fn bubble_sort(numbers: &mut Vec<i32>) {
    let mut sorted = true;
    for i in 0..numbers.len() {
        sorted = true;
        for j in 0..numbers.len() - 1 {
            if numbers[j] > numbers[j + 1] {
                numbers.swap(j, j + 1);
                sorted = false;
            }
        }
    }
    
    if sorted {
        break; 
    }
}

Merge Sort

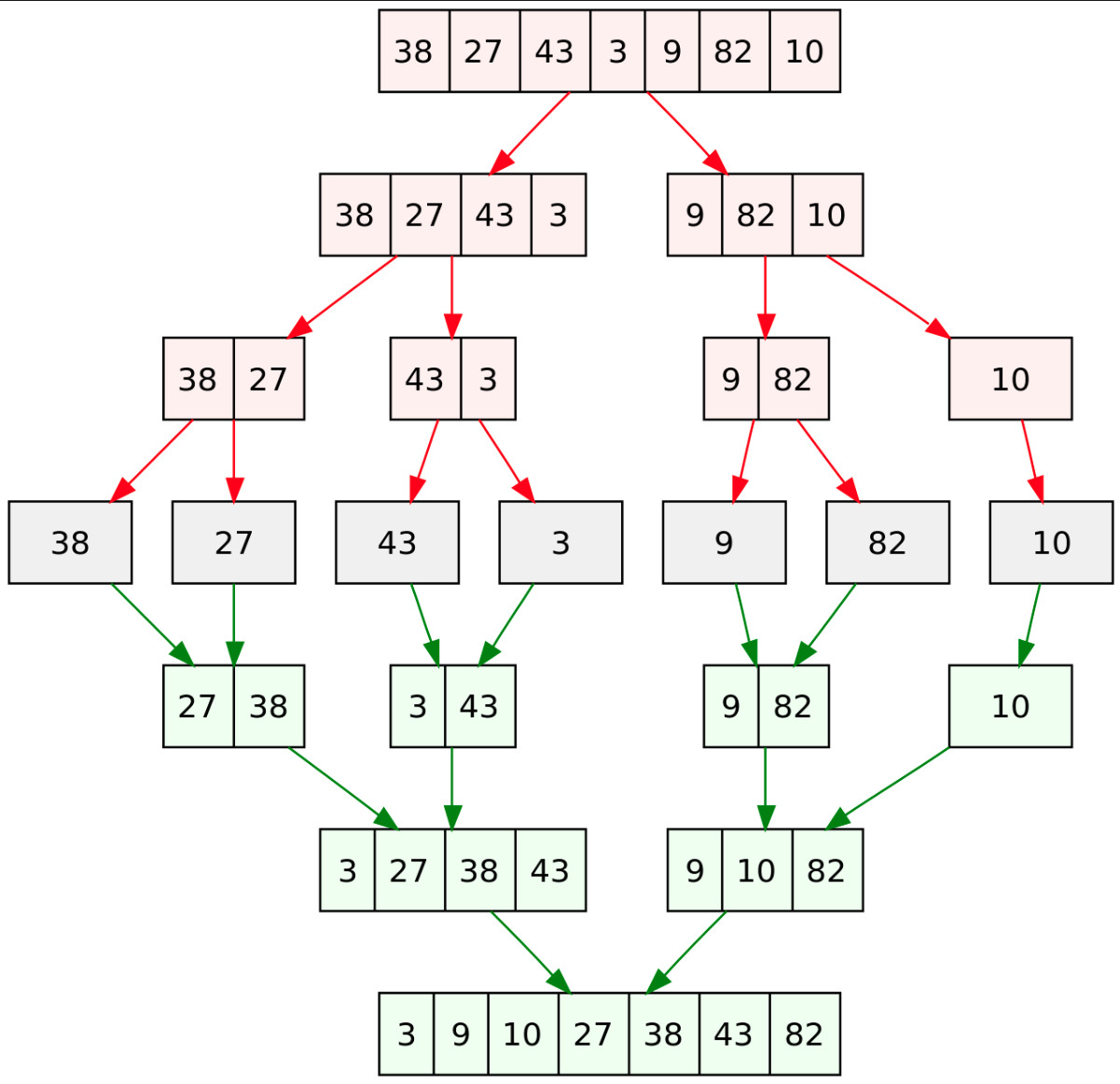
This is more interesting. This is known as a divide and conquer approach as we break the problem up. For this we need to

• Break the array in half until each level is 1 or 2 numbers (4 levels in this picture)
• Create empty array of original length
• Take element either from left of right depending on which is the largest

fn merge_sort(arr: &mut [i32]) -> Vec<i32> {

    // Base case
    if arr.len() > 1 {

        // Split the array into two, left and right
        let mid = arr.len() / 2;
        let left_merge = merge_sort(&mut arr[..mid]);
        let right_merge = merge_sort(&mut arr[mid..]);

        let mut left_index = 0;
        let mut right_index = 0;

        for val in &mut *arr {
            // Determine if left or right index is next
            if right_index == right_merge.len() || (left_index < left_merge.len() && left_merge[left_index] < right_merge[right_index]) {
                // Set left index as next value
                *val = left_merge[left_index];
                left_index += 1;
            } else {
                // Set right index as next value
                *val = right_merge[right_index];
                right_index += 1;
            }
        }
    }

    arr.to_vec()

}

fn main() {
    let mut merge_numbers = vec![38, 27, 43, 3, 9,82, 10];
    let answer4 = merge_sort(&mut merge_numbers);
    println!("This is the answer {:?}", answer4);
}