Sorting in Code: Difference between revisions
Jump to navigation
Jump to search
Created page with "=Sorting= ==Selection Sort== Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python <syntaxhighlight lang="py"> def selection_sort(array): m = len(array) for i in range(m - 1): # Assume the current index (i) has the minimum value min_index = i # Find the minimum element in the remaining unsorted part for j in range(i + 1, m): if array[j] < array[min_index]:..." |
|||
| Line 1: | Line 1: | ||
=Selection Sort= | |||
Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python | Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python | ||
<syntaxhighlight lang="py"> | <syntaxhighlight lang="py"> | ||
| Line 30: | Line 29: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
=Bubble Sort= | |||
This was the first sort I did 40 years ago. Here in rust. Again this is this is O(n²) | This was the first sort I did 40 years ago. Here in rust. Again this is this is O(n²) | ||
<syntaxhighlight lang="rs"> | <syntaxhighlight lang="rs"> | ||
| Line 60: | Line 59: | ||
break; | break; | ||
} | } | ||
} | |||
</syntaxhighlight> | |||
=Merge Sort= | |||
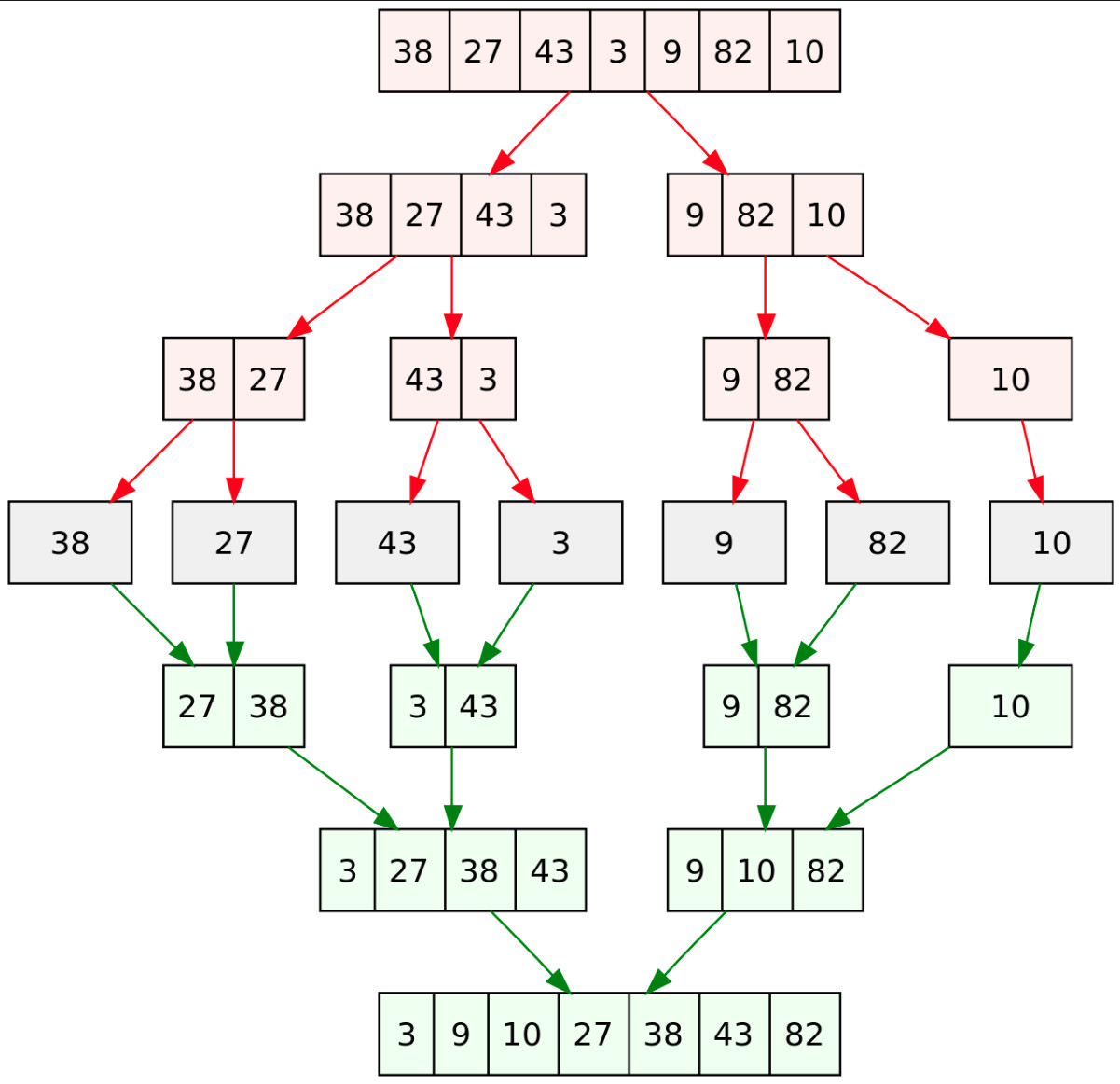
This is more interesting. This is known as a divide and conquer approach as we break the problem up. For this we need to | |||
*Break the array in half until each level is 1 or 2 numbers (4 levels in this picture) | |||
*Create empty array of original length | |||
*Take element either from left of right depending on which is the largest | |||
[[File:Merge sort.jpg | 500px]] | |||
<syntaxhighlight lang="rs"> | |||
fn merge_sort(arr: &mut [i32]) -> Vec<i32> { | |||
// Base case | |||
if arr.len() > 1 { | |||
// Split the array into two, left and right | |||
let mid = arr.len() / 2; | |||
let left_merge = merge_sort(&mut arr[..mid]); | |||
let right_merge = merge_sort(&mut arr[mid..]); | |||
let mut left_index = 0; | |||
let mut right_index = 0; | |||
for val in &mut *arr { | |||
// Determine if left or right index is next | |||
if right_index == right_merge.len() || (left_index < left_merge.len() && left_merge[left_index] < right_merge[right_index]) { | |||
// Set left index as next value | |||
*val = left_merge[left_index]; | |||
left_index += 1; | |||
} else { | |||
// Set right index as next value | |||
*val = right_merge[right_index]; | |||
right_index += 1; | |||
} | |||
} | |||
} | |||
arr.to_vec() | |||
} | |||
fn main() { | |||
let mut merge_numbers = vec![38, 27, 43, 3, 9,82, 10]; | |||
let answer4 = merge_sort(&mut merge_numbers); | |||
println!("This is the answer {:?}", answer4); | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Revision as of 01:59, 10 October 2024
Selection Sort
Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python
def selection_sort(array):
m = len(array)
for i in range(m - 1):
# Assume the current index (i) has the minimum value
min_index = i
# Find the minimum element in the remaining unsorted part
for j in range(i + 1, m):
if array[j] < array[min_index]:
min_index = j
# Swap the found minimum element with the first element of the unsorted part
array[i], array[min_index] = array[min_index], array[i]
Looking at the code there are two for loops meaning this is O(n²)
And here it is in rust
fn selection_sort(numbers: &mut Vec<i32>) {
for i in 0..numbers.len() {
let mut min_index = i;
for j in i..numbers.len() {
if numbers[j] < numbers[min_index] {
min_index = j;
}
}
numbers.swap(i, min_index);
}
}
Bubble Sort
This was the first sort I did 40 years ago. Here in rust. Again this is this is O(n²)
fn bubble_sort(numbers: &mut Vec<i32>) {
for i in 0..numbers.len() {
for j in 0..numbers.len() - 1 {
if numbers[j] > numbers[j + 1] {
numbers.swap(j, j + 1);
}
}
}
}
There were improvements made in the course to the original answer where they identified code repeated even thought we knew the data was already sorted. A clear reason not to just cut and paste.
fn bubble_sort(numbers: &mut Vec<i32>) {
let mut sorted = true;
for i in 0..numbers.len() {
sorted = true;
for j in 0..numbers.len() - 1 {
if numbers[j] > numbers[j + 1] {
numbers.swap(j, j + 1);
sorted = false;
}
}
}
if sorted {
break;
}
}
Merge Sort
This is more interesting. This is known as a divide and conquer approach as we break the problem up. For this we need to
- Break the array in half until each level is 1 or 2 numbers (4 levels in this picture)
- Create empty array of original length
- Take element either from left of right depending on which is the largest
fn merge_sort(arr: &mut [i32]) -> Vec<i32> {
// Base case
if arr.len() > 1 {
// Split the array into two, left and right
let mid = arr.len() / 2;
let left_merge = merge_sort(&mut arr[..mid]);
let right_merge = merge_sort(&mut arr[mid..]);
let mut left_index = 0;
let mut right_index = 0;
for val in &mut *arr {
// Determine if left or right index is next
if right_index == right_merge.len() || (left_index < left_merge.len() && left_merge[left_index] < right_merge[right_index]) {
// Set left index as next value
*val = left_merge[left_index];
left_index += 1;
} else {
// Set right index as next value
*val = right_merge[right_index];
right_index += 1;
}
}
}
arr.to_vec()
}
fn main() {
let mut merge_numbers = vec![38, 27, 43, 3, 9,82, 10];
let answer4 = merge_sort(&mut merge_numbers);
println!("This is the answer {:?}", answer4);
}